from sklearn.preprocessing import StandardScaler, Normalizer
from sklearn.decomposition import PCAfit() : 평균 𝜇과 표준편차 𝜎를 계산
transform() : 정규화/표준화, Standardization
fit_trasform() : fit() + transform()
fit() -데이터를 학습시키는 메서드
transform() - 학습시킨 것을 적용하는 메서드
So, Test data set에는 적용하면 안됨!
= sclaer가 기존에 학습 데이터에 fit한 기준을 다 무시하고 테스트 데이터에 새로운 mean, variance값을 얻으면서 테스트 데이터까지 학습해버린다. 테스트 데이터는 검증을 위해 남겨둔 Set
고유벡터 (Eigenvector) 고유값 (Eigenvalue)
고유벡터는 주어진 transformation에 대해서 크기만 변하고 방향은 변화 하지 않는 벡터
여기서 변화하는 크기는 결국 스칼라 값으로 변화 할 수 밖에 없는데, 이 특정 스칼라 값을 고유값 (eigenvalue)
# 고유 값은 고유벡터 방향으로 얼마만큼의 크기로 벡터공간이 늘려지는 지를 얘기한다
== 예를 들어 지구의 자전운동과 같이 3차원 회전변환을 생각했을 때, 이 회전변환에 의해 변하지
않는 고유벡터는 회전축 벡터이고 그 고유값은 1이 될 것이다.
- transformation에 영향을 받지 않는 회전축, (혹은 벡터)
(= 분산의 방향을 알려줌)
- 변화하는 크기는 결국 스칼라 값으로 변화 할 수 밖에 없는데, 이 특정 스칼라 값을 고유값
(= 설명가능한 분산량)
*Vector transformation은 결국 궁극적으로는 데이터를 변환한다

https://angeloyeo.github.io/2019/07/17/eigen_vector.html
고윳값과 고유벡터 - 공돌이의 수학정리노트
angeloyeo.github.io
np.linalg.norm / inv / eig ## 벡터의 크기(lVl), 역행렬, 고유값과 벡터
( value, vector = np.linalg.eig() )
np.dot/ matmul ## 두 벡터의 내적 주의) 2차원에서는 같지만 3차원부터는 값이다름
np.multiply ## 곱(=스칼라)Explained Variance Ratio은 각각의 주성분 벡터가 이루는 축에
투영(projection)한 결과의 분산의 비율을 말하며, == 각 eigenvalue의 비율
<value, vector = np.linalg.eig()>
*벡터 array로 나오기 때문에 벡터값은 위아래로 읽어야됨 df[:,0] 전체행에서 0번째 열
array([[-0.9057736 , -0.85343697],
[ 0.42376194, -0.52119606]]
Principal Component Analysis (PCA)
<알아야할 개념>
PCA -> 공분산 -> 행렬 -> 벡터의 내적(정사영), 고유벡터, 고유값
- 고차원 데이터를 효과적으로 분석 하기 위한 기법
- 낮은 차원으로 차원축소
- 고차원 데이터를 효과적으로 시각화 + clustering
- 원래 고차원 데이터의 정보(분산)를 최대한 유지하는 벡터를 찾고, 해당 벡터에 대해 데이터를 (Linear)Projection
- 데이터들을 차원 축소시킬 때 가장 원래 의미를 잘 보존
데이터들을 정사영 시켜 차원을 낮춘다면,
어떤 벡터에 데이터들을 정사영 시켜야 원래의 데이터 구조를 제일 잘 유지할 수 있을까?
정사영이란??
https://cord-ai.tistory.com/12
n132 공분산과 상관계수 cov, corr/ vector
분산, 표준편차 * 분산은, 데이터가 얼마나 퍼져있는지를 측정하는 방법 = (관측값과 평균의 차)를 제곱한 값을 모두 더하고 관측값 개수로 나눈 값 = 차이 값의 제곱의 평균 * 분산을 구하는 과정
cord-ai.tistory.com
분석과정
- scikit-learn PCA는 특이값 분해(SVD, Singular Value Decomposition)를 이용해 계산
https://darkpgmr.tistory.com/106
[선형대수학 #4] 특이값 분해(Singular Value Decomposition, SVD)의 활용
활용도 측면에서 선형대수학의 꽃이라 할 수 있는 특이값 분해(Singular Value Decomposition, SVD)에 대한 내용입니다. 보통은 복소수 공간을 포함하여 정의하는 것이 일반적이지만 이 글에서는 실수(real
darkpgmr.tistory.com
1. 가장 분산이 큰 주성분 ~~ 차례로 구함
= 주성분 개수(n_components)를 설정할 때, 몇 개의 주성분을 사용하는 것이 유리할지 임의로 판단하는 것은 어렵다.
따라서, 0~1 사이의 실수를 입려하면 지정된 비율만큼의 분산이 유지되는 최소한의 주성분 개수를 자동으로 선택
# 5% 만큼의 정보(분산)을 잃는다
pca = PCA(n_components=0.95)다차원의 데이터에서 차원 감소를 시켜주는 것이 PCA의 주목적,
그러면 고차원의 데이터를 어디까지 차원감소 시켜주는 것이 타당할까?
EX) N차원의 데이터가 있다고 할때, N개의 eigenvalue를 계산할 수 있는데 누적되는(= np.cumsum()) Eigenvalue의 합이,
90%이상 or 근접하면 해당 차원까지 줄이는 것이 타당함
2. PC(주성분)은 서로 직교함(= 공분산 행렬의 고유벡터이므로) == 상관계수 0 / 서로 의미가 없다는 뜻
3. 단위 스케일링이 필요함 => 표준화 / 평균0, 분산1
4. 분산 공분산 matrix를 만듬
고유 벡터는 그 행렬이 벡터에 작용하는 주축(principal axis)의 방향을 나타내므로 공분산 행렬의
고유 벡터는 데이터가 어떤 방향으로 분산되어 있는지를 나타내준다고 할 수 있다.
데이터 벡터를 어떤 벡터에 내적(혹은 정사영)하는 것이 최적의 결과를 내주는가?’
5. 고유값과 고유벡터를 구함(= 표준화하게 되면 총분산은 갯수만큼 값이 나옴, 2개의 변수면 총분산도 2)
고유 값이 큰 순서대로 고유 벡터를 정렬하면 결과적으로 중요한 순서대로 주성분을 구하는 것이 된다.
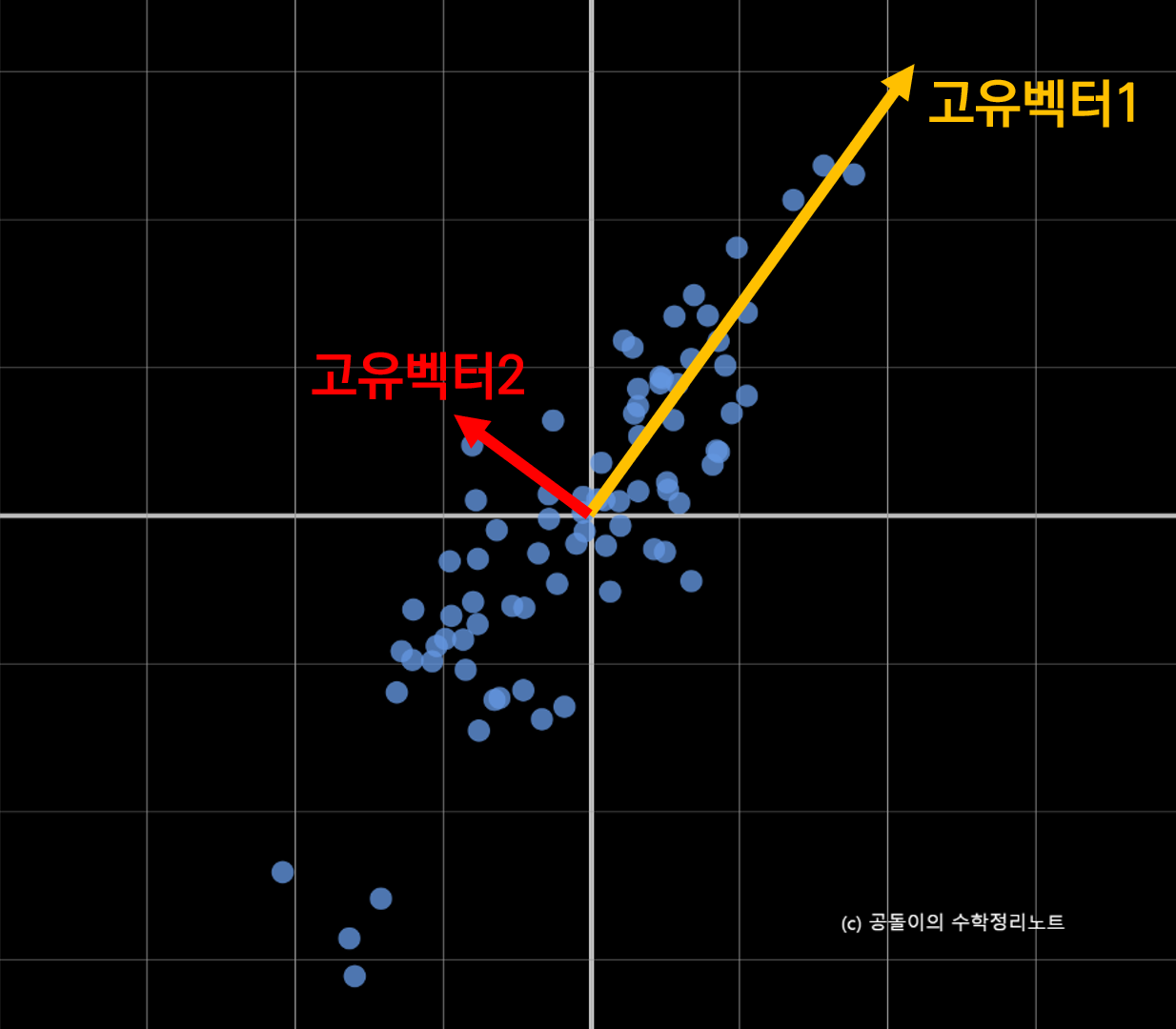
고유 벡터 두 개를 볼 수 있고 각각의 벡터의 크기가 각 벡터의 고윳값을 의미한다.
6. 나온 PC값과 변수와 상관관계를 봄(= 고유값/변수 개수 ==> 각 변수의 상관관계)
( 먼저 변수사이에 상관관계를 보면서 '이 주성분은 무엇이다'라고 칭한다고 가정을 함)
7. 투영(projection) 값이 작은 값 기준으로 봄
https://angeloyeo.github.io/2019/07/27/PCA.html
주성분 분석(PCA) - 공돌이의 수학정리노트 (Angelo's Math Notes)
angeloyeo.github.io
Code
from sklearn.preprocessing import StandardScaler, Normalizer
from sklearn.decomposition import PCA
#먼저 데이터 표준화 시킴(= 단위 스케일링) , 정규화 = 분산
scaler = StandardScaler()
Z = scaler.fit_transform(data_f)
print("\n Standardized Data: \n", Z)
pca = PCA(2) # n_componets == 주성분 개수
pca.fit(Z) # Z를 가진 모델로 맞춘다
# pca.components == 고유벡터
print("\n Eigenvectors: \n", pca.components_)
# Eigenvalues == 고유값
print("\n Eigenvalues: \n",pca.explained_variance_ )
ratio= pca.explained_variance_ratio_
print(ratio)
# 주성분 비율
[0.68633893 0.19452929]
## cumsum은 배열에서 주어진 축에 따라 누적되는 원소들의 누적 합을 계산하는 함수.
'''
a = np.array([[1,2,3], [4,5,6]])
print(np.cumsum(a)) # (axis=0, 1) ==> axis에 따른 누적합
[ 1 3 6 10 15 21]
'''
cumsum = np.cumsum(pca.explained_variance_ratio_)
d = np.argmax(cumsum >= 0.95) + 1
print('선택할 차원 수 :', d)
Standardized Data:
[[-0.89604189 0.7807321 -1.42675157 -0.56847478]
[-0.82278787 0.11958397 -1.06947358 -0.50628618]
[-0.67627982 0.42472926 -0.42637319 -1.1903608 ]
...
[ 1.17338426 -0.74499437 1.50292796 1.91906927]
[ 0.22108196 -1.20271231 0.78837197 1.23499466]
[ 1.08181673 -0.54156417 0.85982757 1.48374906]]
Eigenvectors:
[[ 0.45375317 -0.39904723 0.576825 0.54967471]
[ 0.6001949 0.79616951 0.00578817 0.07646366]]
'''
주성분 비율이 ==> 두 pc1, pc2 값의 합이 0.88 이상 즉, 두 개의 주성분이 전체 분산의 약 88%
따라서, 추가적인 주성분을 투입하더라도 설명 가능한 분산량이 얼마 증가하지 않기 때문에
주성분은 두 개로 결정하는 것이 적절하다고 할 수 있다.
'''
# pca.transform(df) ## 투영한(=주성분 점수들) 값(= np.matmul(matrix, vector) )
B = pca.transform(Z)# PCA Projection to 2D
D = pd.DataFrame(data= B, columns= ['pc1', 'pc2'])
# 주성분 점수간의 상관계수
D.corr() #주성분 점수간의 상관계수 = 0 ==> 직각이니까Scree Plot
## 그래프
fig, ax= plt.subplots(figsize=(10,8))
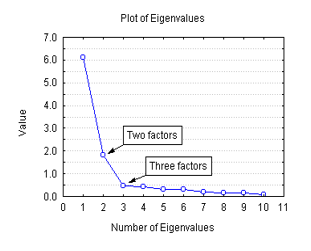
plt.plot(pca.explained_variance_, 'o-') ## screeplot 확인
'''
그래프에서 특정 구간부터 갑자기 꺾이는 부분까지 차원 감소를 시켜준다
scree plot은 PCA외에도 많은 method에서 사용된다.
'''
Feacture Selection:
Feature Selection이란 데이터셋에서 덜 중요한 feature를 제거 하는 방법
Feature Extraction
- 기존에 있는 Feature or 그들을 바탕으로 조합된 Feature를 사용 하는 것
Selection 의 경우
- 장점 : 선택된 feature 해석이 쉽다.
- 단점 : feature들간의 연관성을 고려해야함.
- 예시 : LASSO, Genetic algorithm 등
Extraction의 경우
- 장점 : feature 들간의 연관성 고려됨. feature수 많이 줄일 수 있음
- 단점 : feature 해석이 어려움.
- 예시 : PCA, Auto-encoder 등
'Data Analysis, DA > Linear Algebra' 카테고리의 다른 글
| Log Transform (0) | 2023.05.31 |
|---|---|
| n134 Clustering 군집분석 (0) | 2021.05.29 |
| n132 공분산과 상관계수 cov, corr/ vector (0) | 2021.05.27 |
| n131 벡터와 행렬(vector and matrices)/ 선형대수 (0) | 2021.05.22 |



댓글