ds_before =
pd.read_csv('https://ds-lecture-data.s3.ap-northeast-2.amazonaws.com/seoul_tree/seoul_tree.txt',
sep='\t', skiprows= 1) #skipprow 맨 처음 행 제외하고 보여줌 // thouusands= ',' 콤마 미리 없애
*기술 통계치(Descriptive Statistics)란?
- 평균(mean), 중앙값(median), SD(표준편차, Standard Devidation= 평균에서 떨어진 정도) 등을(통계치) 계산한 것
- count, mean, standard dev, min, 1Q, median, 3Q, max ==> DataFrame.describe()
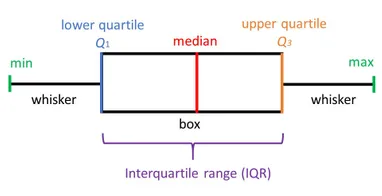
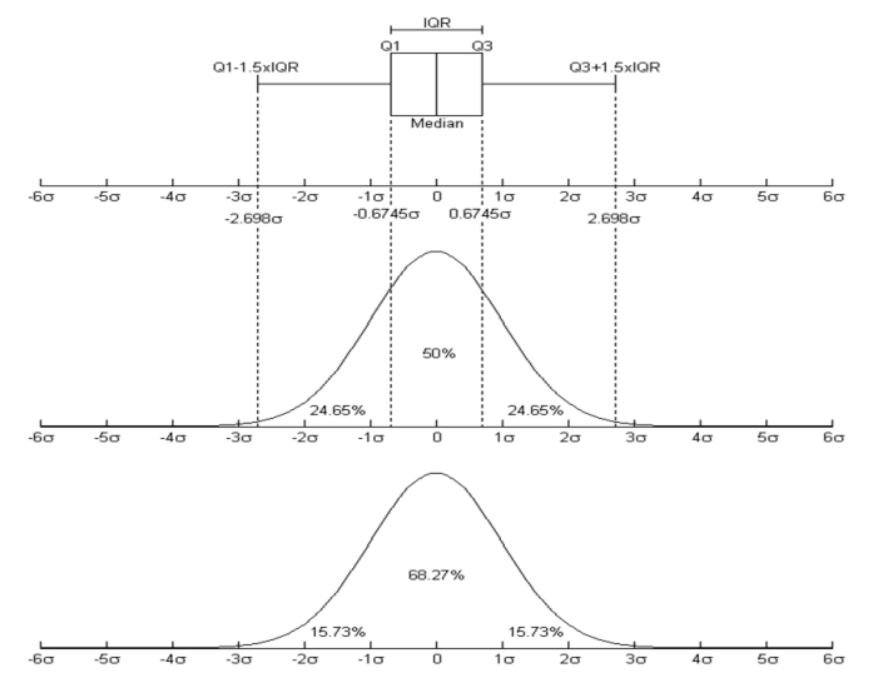
- boxplot

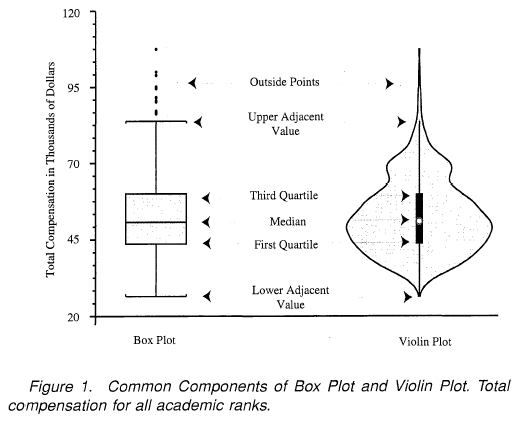
- violin plot
*추리 통계치(Inferetial Statistics)란?
= 모집단을(population)에서 자료를 얻기란 쉽지 않기 때문에(여러 조건..돈, 시간)
거기서 표본을(sample)을가져와 추리 통계치를 계산함
일반적으로 모집단이 정규분포라면 표본의 평균의 분포는 정규분포를 이룬다
np.random.seed(1111) 랜덤값을 저장 (1111)
np.random.randint(0, 100, 20) ==> *randint 100개중에 20개를 무작위로 뽑아
==> np.random.randint(최소, 최대=None, 갯수=None)
매개변수 = low, high, size, dtype
====> .tolist() 매트릭스 array 생성
rand : 0과 1 사이에서 균일하게 분포된 난수들을 생성 (uniform random number) = matrix array 생성
== > np.random.rand(10), np.random.rand(100) --> 각각 10, 100개 생성
np.random.rand(3, 2) = 3행 2열로
randn : 평균이 0이고 표준편차(분산)가 1인 표준정규분포 난수들의 생성 (gaussian random number)
= matrix array생성 >>> -1 0 1
normal : 정규분포에서 무작위 샘플
uniform: 균등분포
suffle : 순서를 바꾸기
choice : 기존 데이터 sampling = matrix array 생성//
np.random.choice(ds.index, size = 10)
DataFrame.loc[np.random.choice] // matrix array ==> 데이터프레임화 해줌*모수란, Parameter?
- 평균
- 분산, 표준편차
- 분위수 (중위값, 1분위수, 4분위수 등…)
- 모비율
편차 - 관측값에서 평균 또는 중앙값을 뺀 것
분산 - 차이값(=편차)의 제곱의 평균
표준편차 - 분산의 제곱근
추측 통계학의 개념으로는 전체(모집단)의 일부(표본)을 살펴서 전체를 알려고 하는 것.
(= 모집단의 특성을 보여주는 값)
전체 집단의 모든 데이터를 알지 못하더라도 수학적으로 그 분포를 기술할 수 있는 특성값들을 알 수만 있다면 “얼추 비슷하게나마” 모집단의 특성을 통계적으로 확인할 수 있다. 이 특성들을 모수(Parameter)라고 부른다.
알맞은 표본의 크기를 결정하려면???
https://www.qualtrics.com/kr/experience-management/research/determine-sample-size/
올바른 표본 크기를 설정하는 방법
표본 크기를 계산하기 전, 표적모집단과 필요한 정확도 수준에 대해 몇 가지를 결정해야 합니다.
www.qualtrics.com
표본 평균의 표준 오차 ( Standard Error of the Sample Mean )
# 더 많은 정보 -> 무작위성을 고려하더라도 더 높은 신뢰성 / sample size가 커야함
pd.DataFrame(np.random.binomial(n = 1, p = 0.5, size = 100)).hist();
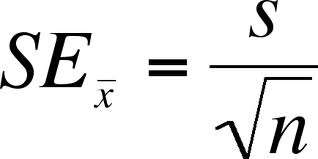
s (우측) = 표본의 표준편차 (sample standard deviation)
n = 표본의 수 (sample size)
<표본의 크기 vs 표본의 개수>
표본의 크기 = 표본의 원소의 개수
조사자 50(표본의 개수) = 각 조사자 당 1000명 조사(표본의 크기)
people1(표본) = {p1,p2,p3,...p1000}
people2(표본) = {p1,p2,p3,...p1000}
...
https://hsm-edu.tistory.com/1104
표본의 크기 vs 표본의 개수
표본의 크기와 개수가 헷갈리신다는 분들이 많이 계셔서 이번 글에서 설명을 해보려고 합니다. 한가지 예시로 쉽게 이해할 수 있을 겁니다. 아래와 같은 모집단이 있다고 합시다. 모집단 = {a,b,c,
hsm-edu.tistory.com
Sampling 기법
샘플링이란 표본추출을 의미하는 것으로, 모집단 전체에 대한 추정치(estimate)를 얻기 위해 임의의 sample을 뽑아내는 것이다.
모집단 전체에 대한 조사는 불가능하기 때문에 sample을 이용하여 모집단에 대한 추론(inference)을 하게되는 것이다. 하지만 표본은 모집단을 닮은 모집단의 mirror image 같은 존재이지만, 모집단 그 자체일수는 없다. 따라서 표본에는 반드시 모집단의 원래 패턴에서 놓친 부분, 즉 noise가 존재할 수 밖에 없다.
- Simple random sampling = 무작위
- Systematic sampling = sampling 할때 규칙을 가지고 추출
- Stratified random sampling = 모집단을 미리 여러그룹으로 나누고 그룹별로 무작위 추출
- Cluster sampling = 집단을 미리 여러그룹으로 나누고 특정 그룹을 무작위로 추출
Resampling
https://cord-ai.tistory.com/22
n224 Cross Validation / K- hold out / TargetEncoder
모델선택을 위한 교차검증 방법을 이해하고 활용할 수 있다. 하이퍼파라미터를 최적화하여 모델의 성능을 향상시킬 수 있다. 왜 train validation test로 나누나? * 모델 선택 ( Model Selection ) 우리 문제
cord-ai.tistory.com
*평균값
- 자료를 대표하는 값
- 모든 자료로부터 영향을 받아/ 즉, 이상한 값의 영향을 받기 쉽다(아웃라이어에 취약하다)
- 평균값이 있어야 분산 or 표준편차 계산 가능
*분산
- 평균값을 기준으로(중심) 퍼져있는 평균적인 거리
*가설 검정 ( Hyphothesis )
- 주어진 상황에 대해서, 하고자 하는 주장이 맞는지 아닌지를 판정하는 과정.
- 모집단의 실제 값에 대한 sample의 통계치를 사용해서 통계적으로 유의한지 아닌지 여부를 판정함.
- ===> 여기서 유의하다는 뭔가 이유가 있다 즉, 귀무가설이 아닌 대안가설(차이가 있는 이유가 있다) p < 0.05
*T-test Process == 평균값으로 같은지 다른지 판별 // 평균 분석
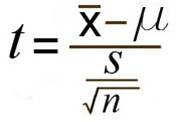
차이가 큰지 작은지를 판별하기 어렵기 때문에 비교대상인 표준편차=분산이 필요함
평균값과 표준편차를 비교하여 가설 판별
- 귀무가설(Null Hyhothesis) 설정
- 대안가설/대립가설 ( altermative '')
- 신뢰도 설정 (confidence Level)
- P-value 확인 (= 0~1사이에 확률값)
https://brunch.co.kr/@jihoonleeh9l6/33
통계, t-test에 대해 알아보자(R)
디자인과 논문 작성에 필요한 통계를 알아보자. | 디자이너들이 논문을 적을 때 가장 어려워하는 부분이 통계이다. 귀무가설이란 무엇인지, 통계적으로 유의미함은 무엇인지, t-test는 무엇인지,
brunch.co.kr
가설 설정은 위에서 언급했던 귀무 가설과 대립 가설을 설정하는 것을 말합니다. 예로들어 'A반에서 새로운 교육법을 도입했더니 학생 성적이 올랐다' 라는 가정을 검증하고 싶다고 합시다. 만일 새로운 교육법이 학생들의 성적이 올렸다면 기존 교육법에서 새로운 교육법을 도입했을 시 각 평균 성적의 차이가 날 것이라 예상할 수 있습니다. 이 차이를 수치적으로 귀무가설은
H0 : Mean(기존) - Mean(새로운) = 0
라고 할 수 있으며, 대립 가설은
H1 : Mean(기존) - Mean(새로운) ≠ 0
라고 정의할 수 있습니다. 또한 위에서는 서로 다른 것만 비교하면 되는 것이므로 검정방법 중 양측검정을 수행하게 됩니다. 만일 대소 비교를 한다고 하면 단측검정을 수행해야 할 것입니다.
가설 검정은 귀무가설 H0가 맞다는 전제하에 진행되게 되며 이 H0가 맞다고 가정할 시 나올 확률이 매우 적은 표본통계값이 나오게 될 시에는 이 가설을 기각하고 대립가설을 채택하는 형식으로 검정 절차가 진행되게 됩니다.
출처: https://engkimbs.tistory.com/758 [새로비:티스토리]
P-value 는, 주어진 가설에 대해서 "얼마나 근거가 있는지"에 대한 값을 0과 1사이의 값으로 scale한 지표 이며 p-value가 낮다는 것은, 귀무가설이 틀렸을 확률이 높다.
* 0.05 ~ pvalue ~ 0.1 사이인 경우: (애매함)
- 실험을 다시한다.
- 데이터를 다시 뽑는다.
- 샘플링을 다시한다
- 기존의 경험 / 인사이트를 바탕으로 가설에 대한 결론을 내린다.
from scipy import stats
*one sample t-test (평균이 특정값과 동일한지) stats.ttest_1samp(x, 비교 평균값)
*two sample t-test (두집단의 평균이 서로 동일한지) stats.ttest_ind(x, y)
*paired(?) t-test (대응 두집단) stats.ttest_rel(x, y)
== 사후검정 ex)복부 수술전 9명의 몸무게와 복부 수술후 몸무게 변화paired t-test???
<t-test를 하기 위한 조건>
1. 표본이 독립적인가?? 아니라면 paired t-test
2. 수집된 데이터가 정규 분포를 따르는가?? 아니라면 Wilcoxon test
3. 집단이 두개인가?? 아니라면 ANOVA
독립적이란?
서로 다른 두 집단에서의 표본을 추출하고 어떤 실험을 진행했다. (독립적)
어떤 집단에서 표본을 추출하고 연속된 두 가지 실험을 진행했다. (표본이 독립되지 않았다)
*큰 수의 법칙 ( Law of large numbers )
sample 데이터의 수가 커질 수록, sample의 통계치는 점점 모집단의 모수와 같아진다.
*One-side test vs Two-side test
two side (tail) test : 샘플 데이터의 평균이 "X"와 같다 / 같지 않다. 를 검정하는 내용 =단측검정 p
0.05 / 5%
one side test : 샘플 데이터의 평균이 "X"보다 크다 혹은 작다 / 크지 않다 작지 않다. 를 검정하는 내용 = 양측검정 p/2
0.025 / 2.5% ==> 나온 p값/2 와 0.025와 비교 ==>하는 것은 맞지만 유의수준이 0.05인건 변하지 않음 그래서 그냥 비교해도 무방 p / 0.05
*******************************************************************
#!pip install --upgrade seaborn scipy == 최신버전으로 업그레이드
print(stats.ttest_ind(a,b, alternative= 'greater'))
== a,b 순서 중요함 a가 b 보다 더 크다라는 가설
#alternative 대안가설
stats.ttest_ind(x, y) 후 p value에서 p/2 > 0.025 ==> 아니라 0.05로 비교해야됨 왜? 귀무가설이 옳다 볼수 있다.
print(stats.ttest_ind(a,b, alternative= 'less'))
print(stats.ttest_ind(a,b, alternative= 'two-sided'))
= 모수가 신뢰 구간 안에 포함될 확률이 95%
= 귀무가설이 틀렸지만 우연히 성립할 확률이 5%

<신뢰구간>
https://cord-ai.tistory.com/10
N123 중심극한정리( Central Limit Theorem, CLT)
*중심극한정리 ( Central Limit Theorem, CLT ) - sample 데이터의 수가 많아질 수록, sample의 평균은 정규분포에 근사한 형태로 나타난다. *큰 수의 법칙 ( Law of large numbers ) sample 데이터의 수가 커질 수록, sa
cord-ai.tistory.com
*ANOVA One - way
*ANOVA 분산분석 // 집단간 분석 + 집단내 분석 (두개 이상의 집단을 비교할때)
3개의 평균값이 같은지/ 다른지 = f-value가 크면 다르다?? 어느하나는 다르다 볼 수 있음
평균들의 값이 서로 다른 값 중에 유의한 값을 나타내는지 검증하기 위해
독립(independent)변수 - 인과관계에서 원인이 되는것 = 연속형변수
종속(denpendent)변수 - 인과관계에서 결과가 되는것 = 범주형/이산형 변수(Discret, Categorical)
= (변화에 따라 어떻게 변하는지 알고싶은 변수)
통계변수 - 변수 이외의 것 / 기본적으로 독립변수와 동일하지만...
one way ANOVA (f-value 두 개의 분산이 비율// 평균값이 두가지가 필요 = 전체 평균, 각 그룹의 평균)
- 독립변수가 종속변수에 영향이 있냐를 봄 (독립변수는 무조건 하나 = 하나에서 여러개로 분류가됨)
- 독립변수는 방법 / 종속변수는 주제로 보면됨
첫번째 분산 = Between Variance 그룹간의 차이 ( 전체 평균을 기준으로)- 이게 크다는 것은 각 그룹간의 전체평균과의 거리가 멀다/ 적어도 한그룹의 평균은 다른 그룹의 평균과 다를 수 있다. 우연히 클 가능성을 판단하는 것이 within Variance
두번째 분산 = within Variance 그룹내의 분산 ( 불확실도)
***f -value = Between / within == t -value와 비슷함 but 분모가 분산이냐 불확실도냐에 따라 다름
즉, 그룹간의 차이가 클수록 f- value가 커짐 = 한 그룹의 평균값이 전체평균과는 다르다고 할 수 있음
f- value ==> 값이 커질 수록 대립가설이 됨/ p-value가 0.05보다 작다가 나옴

from scipy.stats import f_oneway
stats.f_oneway(x1, x2, x3)
return
#statistic :float
#The computed F statistic of the test.
#pvalue :float
#The associated p-value from the F distribution.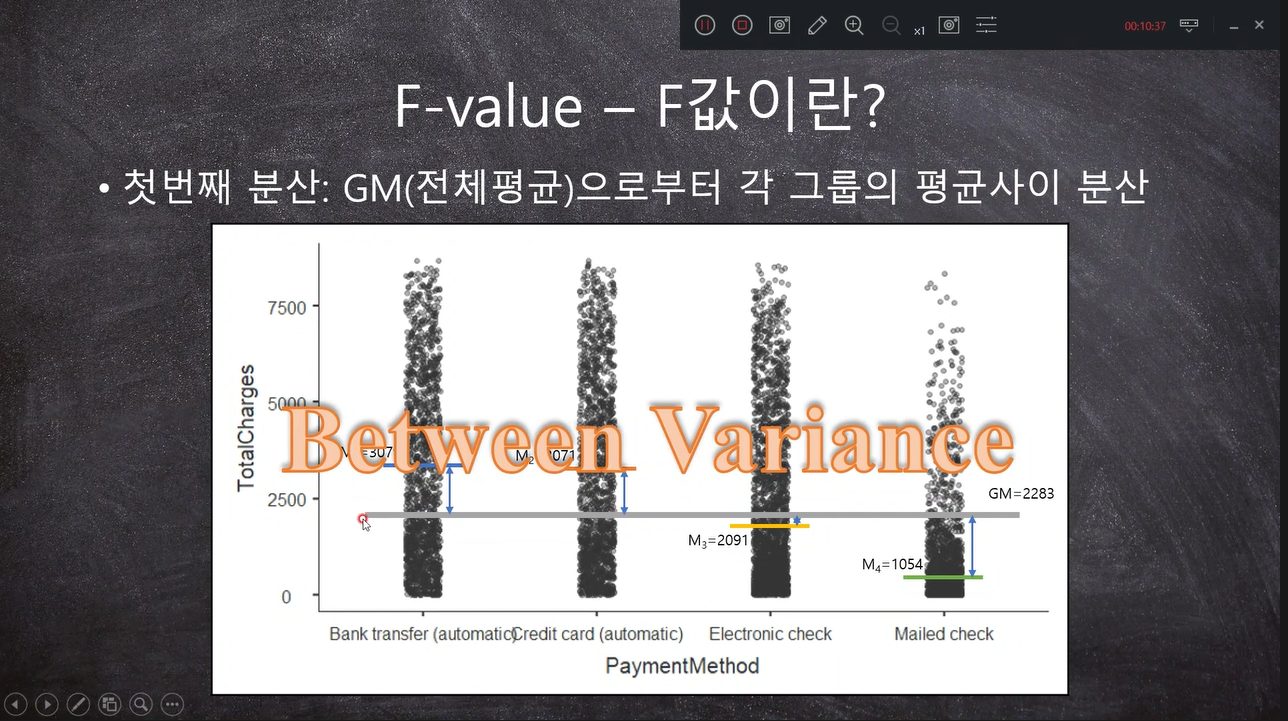

https://www.youtube.com/c/SapientiaaDei
'Data Analysis, DA > statistics' 카테고리의 다른 글
| N123 중심극한정리( Central Limit Theorem, CLT) (0) | 2021.05.19 |
|---|---|
| N124 'Bayes Theorem' (0) | 2021.05.18 |
| N122 T-test++(카이제곱) (0) | 2021.05.15 |



댓글